Astrodynamics
Astrodynamics research deals with the modelling, estimation and planning of spacecraft’s orbits and attitude configurations.
Using cutting-edge astrodynamics techniques, our Space Trajectory Analysis Group (STAG) aims at enabling and supporting space exploration by better understanding, estimating, and controlling the motion of objects in space.
Our mission
The goal of our group is to exploit the chaotic dynamics of the solar system and optimal control theory in order to reduce mission costs and enable innovative mission concepts. We apply our research to a variety of problems, including low-thrust and impulsive interplanetary transfers, spacecraft formation flying, satellite navigation, and remote sensing missions.
The work done by our group is multidisciplinary by nature and span across a variety of STEM disciplines. We attract mathematicians looking at non-linear dynamical problems, electronic engineers for the design and integration of hardware for the testing of our algorithms, software engineers for the development of complex AOCS software systems and computer scientists interested in behavioural models for the scheduling and cooperation of multiple spacecrafts.
Research lead

Dr Nicola Baresi
Senior Lecturer in Orbital Mechanics
Numerical continuation in astrodynamics
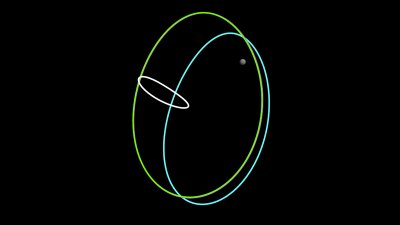
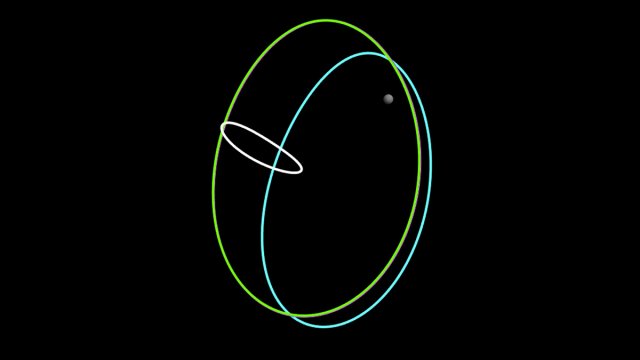
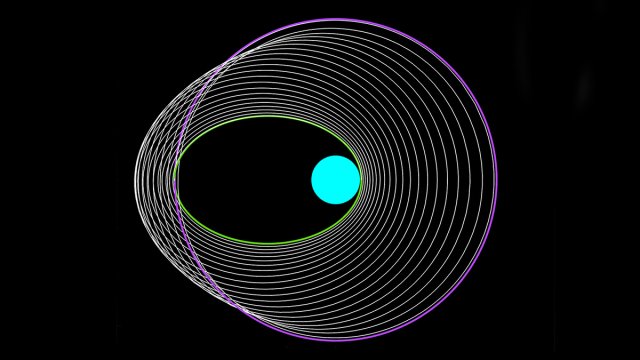
Understanding the motion of objects in space is a core area of space engineering that underpins and enables space exploration. Yet, except for very few occasions (Kepler’s two-body problem and Euler’s attitude equations under torque-free motion assumptions), the evolution of a satellite’s orbit cannot be known in closed-form.
We research into advanced numerical continuation techniques that can help us better understand and organise the dynamics of high-fidelity astrodynamics problems via entire families of periodic and quasi-periodic orbits. Dynamical “highways’’ known as stable and unstable manifolds that emanate from some of these solutions are also leveraged by our team in order to identify ballistic transfers for lunar and deep-space exploration.
Spacecraft trajectory optimisation
Launching a spacecraft is expensive. Improving the efficiency of any spacecraft mission is a key objective of any space mission analyst. This can be achieved by optimising the orbital transfers required to achieve the operative orbit, thus allowing the minimisation of the propellant mass.
We apply optimal control theory to a range of different trajectory optimisation problems including rendezvous and docking; impulsive and low-thrust transfers in two- and three-body problems; orbit maintenance of periodic and quasi-periodic orbits and interplanetary trajectory design.
Orbit and attitude determination

Similarly to our smartphones, which can help us pinpoint our location on Earth via embedded GNSS receivers, satellites in low Earth orbit can also use GNSS constellations (GPS, Galileo, GLONASS,…) to triangulate their position in space. However, things become a lot trickier when GNSS constellations cannot be relied upon or communications with Earth ground stations become difficult owing to physical and/or budget constraints.
By merging knowledge from a variety of engineering topics (probability and statistics, estimation theory, data fusion and processing, computer vision and machine learning), our team aims at analysing orbit and attitude data in order to estimate the position, velocity, and attitude coordinates of a satellite. Our goal is to advance absolute and relative navigation techniques for effective and autonomous estimation algorithms that enable spacecraft operations. These include (but are not limited to) square-root information and unscented Kalman filters for active debris removal and small body exploration missions.
Spacecraft formation flying

An emerging trend in space mission design is the replacement of large monolithic spacecraft with a group of small cost-effective satellites that cooperate in space to fulfill modern and innovative mission objectives. Pivotal to the success of this trend (as well as of related topics such as active debris removal) is a deep understanding of the relative dynamics (orbital and attitude alike) between two or more vehicles in strongly perturbed dynamical environments.
We combine our multi-disciplinary background with Surrey Space Centre’s ad-hoc research facilities to improve upon existing methods of spacecraft formation flying and advance new and disruptive technologies for robust, fuel-efficient, and autonomous proximity operations.
Space mission analysis and design

Space mission design is a complex problem involving different disciplines, many variables, constraints and, sometimes, even clashing objectives. We apply multi-disciplinary optimisation strategies to engineer optimal solutions to innovative mission concepts and complicated trajectory problems.
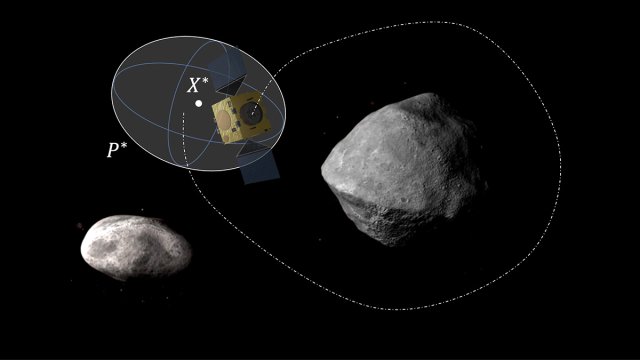
Applications include trajectory design near small irregular bodies (asteroids, comets, and small planetary moons); feasibility studies of small scientific missions under trajectory, payload, and system constraints; active debris removal and space debris observation strategies and interplanetary CubeSats.
Collaborations
Our group has had a long association with Surrey Satellite Technology Ltd (SSTL) and contributed to the successes of many spacecraft missions in the orbit and attitude maintenance of the Surrey Space Centre and SSTL satellites. Our research has also been funded by other private and public organisations including the UK Space Agency (UKSA), the European Space Agency (ESA), and the French space agency (CNES).
Research projects
Meet the team

Dr Alesia Herasimenka
Surrey Future Fellow

Wojciech Kalinowski
Postgraduate Research Student

Ioannis (John) Papuodos
Postgraduate Research Student