Data science and statistical design

Design of experiments concerns the planning of a task to describe or explain the relationship between factors affecting a process. In other words, it is used to find cause-and-effect relationships and to compare treatments. Experimental design has a role in areas such as drug development, horticultural research and industrial processes. Research areas led by Janet Godolphin include design robustness and construction of factorial and fractional factorial designs.

Robustness against design breakdown

Nuisance factors (for example batches of raw material in a manufacturing process) affect a response but are of no intrinsic interest. Blocking is used to eliminate the effect of nuisance factors on treatment comparisons, i.e. on the comparisons that are of interest. It is generally straightforward to obtain a blocked design with ‘good’ properties. However, observations can be lost during experimentation so the eventual design may have less desirable properties than the planned design. In the most extreme situation, an eventual design can be disconnected and it will not be possible to compare all treatments. Understanding the mechanism resulting in design breakdown for different design types leads to a design selection approach that incorporates robustness against breakdown through observation loss.

Construction of factorial and fractional factorial designs

Manufacturing processes can involve many factors. Factorial and fractional factorial designs play an important role in optimising multi-factor processes. Research areas concern the use of graph theory to construct designs providing estimates of main effects and of selected interactions when the treatment structure is factorial, both with and without blocking factors.

Recent mathematical research has developed several crime models such as agent-based model (ABM) for urban burglary that incorporate well-known interactions between individual criminals and environment at the neighbourhood level. These models provide an important tool to establish the links between hypothesised criminal behaviours embedded in the models and observed crime data.

Naratip Santitissadeekorn is developing a nonlinear filtering algorithm technique that can statistically merge model predictions with crime data, mathematically modelled a point process, in order to make better projections of future crime patterns such as crime hot spots. His research will also provide a non-invasive tool to quantify some well-known criminal behaviours (eg. near-repeat victimisation).

Data assimilation involves fusing models and data to estimate model parameters or to predict state variables, or both. In order to develop robust algorithms, it is important to understand both the data and the model structure.

Motivated by models of the carbon cycle in forests, project lead Anne Skeldon is analysing and evaluating the performance of data assimilation schemes in the neighbourhood of tipping points.

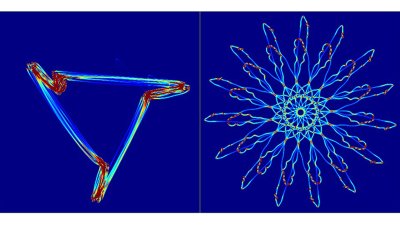
There is much useful diagnostic information in physiological time series, such as electrocardiogram (ECG), continuous blood pressure measurement or photoplethysmography (PPG) signals. However, they are often quite variable, non-stationary and noisy and so can be difficult to process using computational methods.

Conventional methods of analysis consider a reductionist approach such as heart rate variability (HRV) methods that extract the beat-to-beat intervals from a signal and analyse these in a myriad of different ways. Since 1965 over 50,000 research papers have referred to HRV, and this is growing all the time. For ECG signals, certain ‘fiducial points’ are located on the signal from which various intervals and amplitudes are derived, but this process can be difficult for noisy signals.

Philip Aston has led the development of a new approach for analysing ‘approximately periodic’ signals called symmetric projection attractor reconstruction (SPAR), which uses the whole signal without having to reduce it. With this approach, an attractor is created in a three-dimensional phase space using Takens’ delay coordinates. Projecting this attractor onto a two-dimensional plane reduces the effect of baseline wander in the signals and creates a colourful (and pretty!) attractor image. Using these attractor images, changes in the waveform morphology and variability can easily be detected. They can also be used as input for machine/deep learning to detect various conditions from the signals.